数学是一门神奇的学科,同时也充满挑战性,很多人对数学望而生畏,因此部分同学在选择考研时尽量避开数学。其实,数学没有那么神秘而艰难,这在我们每年的数学满分者中可见端倪,而其他科目,如政治、英语,根本就没有出现过满分。这一点充分说明,考研数学是有章可循的,只要方法得当、复习充分、持之以恒,取得高分绝不是痴人说梦。
考研数学要求考生比较系统地理解数学的基本概念和基本理论,掌握数学的基本方法,具备抽象思维能力、逻辑推理能力、空间想象能力、运算能力和综合运用所学的知识分析问题和解决问题的能力。下面老师带领同学们学习一道函数极限的真题,让同学们体会考研数学对综合能力的考查。
这道题目来源于2008年全国硕士研究生入学统一考试数学(一)试题的第15题。
首先,我们一起看一下这道题目:求极限.
这道题考查的是极限求法的综合运用,解法很多,下面我们一起看一下几种具体的解法:
解法一: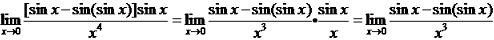
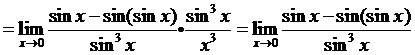
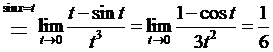
说明:该解法先利用了重要极限 ,然后利用替换法和洛必达法则求解。
,然后利用替换法和洛必达法则求解。
解法二: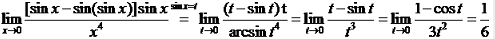
.
说明:该解法先用了替换法,然后利用等价无穷小替换和洛必达法则求解。
解法三:由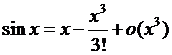 ,得
,得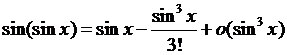 ,于是
,于是 ,故
,故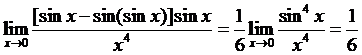 .
.
说明:该解法主要用泰勒公式求解。
解法四: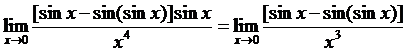
函数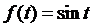 在
在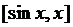 上由拉格朗日中值定理知,
上由拉格朗日中值定理知,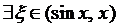 ,使
,使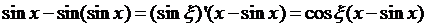 ,
,
则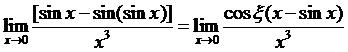 ,又
,又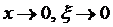 ,则
,则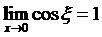 ,所以
,所以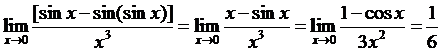 .
.
说明:该解法利用了等价无穷小替换、拉格朗日中值定理及洛必达法则求解。
这道真题的多种解法,体现了考研真题的灵活性。详细分析每种解法,发现每种解法都是多种方法的结合使用,体现了考查目标对广大考生的要求。
通过这道题的分析,同学们应该对考研数学的考查形式有了一定的深入了解,对解题方法的多样性也有了深刻的认识。这就要求同学们在平时的复习中,既要掌握基本方法的运用,又要提高综合运用知识的能力。所以,在数学整学年的复习中,同学们首先要打牢基础,然后构建起全面的知识结构体系和掌握多种重要的方法与结论,最后通过不断地巩固与练习,将所学的知识熟练地应用到具体题目中。只有这样循序渐进,不断地总结与归纳,有目标、有方向地学习,才能在考研数学的考试中取得高分。
(来源:文都教育)

 分享到人人
分享到人人 分享到QQ空间
分享到QQ空间










 恭喜你,发表成功!
恭喜你,发表成功!

 !
!





















