眾所周知,函數求極限是高等數學中最基礎的內容,並且是每年考研數學的必考內容。所以各位考生一定要將極限問題琢磨透了,才能保証在這類考察基礎知識的題目上不丟分。

有的題目是以直接求極限的形式出現,例如2011年數學一的15題:求極限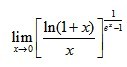 ﹔也有的題目是間接涉及到求極限問題,例如2012年數學一的1題是要求曲線漸近線的條數,求曲線漸進線最終還是通過求函數極限來達到的。這兩類題目在歷年考研數學試題中出現的頻率都很高,求極限的方法一定要熟記於心、熟練掌握,不可輕視!
﹔也有的題目是間接涉及到求極限問題,例如2012年數學一的1題是要求曲線漸近線的條數,求曲線漸進線最終還是通過求函數極限來達到的。這兩類題目在歷年考研數學試題中出現的頻率都很高,求極限的方法一定要熟記於心、熟練掌握,不可輕視!
求極限的方法不隻限於兩三種,概括來講共有下面八大“必殺技”需要掌握:
定義法
此法一般用於極限的証明題,計算題很少用到,但仍應熟練掌握,不重視基礎知識、基本概念的掌握對整個復習過程都是不利的。
洛必達法則
此法適用於解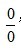 型和
型和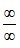 型等不定式極限,但要注意適用條件(不只是使用洛必達法則要注意這點,數學本身是邏輯性非常強的學科,任何一個公式、任何一條定理的成立都是有使其成立的前提條件的,不能想當然的隨便亂用),如出現的極限是形如
型等不定式極限,但要注意適用條件(不只是使用洛必達法則要注意這點,數學本身是邏輯性非常強的學科,任何一個公式、任何一條定理的成立都是有使其成立的前提條件的,不能想當然的隨便亂用),如出現的極限是形如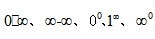 ,則都可以轉化為
,則都可以轉化為 型來求解。
型來求解。
對數法
此法適用於指數函數的極限形式,指數越是復雜的函數,越能體現對數法在求極限中的簡便性,計算到最后要注意代回以e為底,不能功虧一簣。
定積分法
此法適用於待求極限的函數為或者可轉化為無窮項的和與一個分數單位之積,且這無窮項為等差數列,公差即為那個分數單位。
泰勒展開法
待求極限函數為分式,且用其他方法都不容易簡化時使用此法會有意外收獲。當然這要求考生能熟記一些常見初等函數的泰勒展開式且能快速判斷題目是否適合用泰勒展開法,堅持平時多記多練,這都不是難事。
等價替換法
此法能快速簡化待求極限函數的形式,也需要考生熟記一些常用的等價關系,才能保証考試時快速准確地解題。注意等價替換隻能替換乘除關系的式子,加減關系的不可替換。
放縮法(夾逼定理)
此法較簡單,就是對待求極限的函數進行一定的擴大和縮小,使擴大和縮小后的函數極限是易求的,例如《2013考研數學接力題典1800》第4頁的56題:求極限,該題即是用放縮法求解,具體解法可參見書內答案。
重要極限法
高數中的兩個重要極限:及其變形要熟記並學會應用。
掌握了以上八大方法還是不夠的,要學會融會貫通,因為考研題的綜合性很強,不是一道題隻用一種方法就能夠解出來的,往往是同時用到兩三種甚至更多才能順利解答。這就需要考生平時多想多練,做到熟能生巧,才能在最后的考試決戰中勝人一籌。

 分享到人人
分享到人人 分享到QQ空間
分享到QQ空間