對策分析類問題在國考行測中屬於高難度的題型,不僅涉及知識面廣,且解題思路較為繁雜。為了幫助考生解決這一難點,專家將對策分析類問題按考查方向的不同,分為三類:數據分析、統籌問題、推理問題,逐一進行詳細講解。
一、數據分析
數據分析類題目通常給出一些限制條件,在這個條件下數據分布有多種不同組合。題目往往是求這些數據組合的極端情況,其本質是討論數據的離散性。極值一般存在於離散性最差的那種情況。
數據的離散性:(1)常數列(各項相等)離散性最差﹔(2)若各數不相同,公差為1的等差數列離散性最差。
【例題1】某單位2011年招聘了65名畢業生,擬分配到該單位的7個不同部門。假設行政部門分得的畢業生人數比其他部門都多,問行政部門分得的畢業生人數至少為多少名?
A.10 B.11 C.12 D.13
解析:要使分得畢業生人數最多的行政部門人數最少,則其余部門人數盡可能多,即各部門人數盡量接近(可以相等)。從人數最少的選項開始驗証,當行政部門有10人時,其余各部門共有65-10=55人,平均每部門人數超過9人,即至少有1個部門人數超過9人,與行政部門人數最多的題干條件不符。若行政部門有11人,其余部門總人數為54人,每個部門可以是9人,滿足題意,選B。
【例題2】10個箱子總重100公斤,且重量排在前三位的箱子總重不超過重量排在后三位的箱子總重的1.5倍。問最重的箱子重量最多是多少公斤?
A.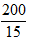 B.
B.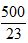 C.20 D.25
C.20 D.25
解析:要使最重的箱子重量盡可能大,其余箱子重量應盡可能小,最極端情況為其余九個箱子重量都相等。設排在后九位的箱子的重量均為x,可知排在第一位的
箱子的重量為1.5×3x-2x=2.5x。因此9x+2.5x=100,解得x= ,最重的箱子的重量為2.5×
,最重的箱子的重量為2.5× 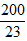 =
=  。
。
綜上所述,數據分析類題目的原則可概括為:組間離散性盡可能大,組內離散性盡可能小,優先考察常數列,各項相異則考慮等差數列。
二、統籌問題
統籌問題研究的是怎樣安排使總用時最短,或總效率最高。歷年國考行測中涉及的統籌問題可分為以下幾類:黑夜過橋問題、排隊問題、任務分配問題、物資集中問題、貨物裝卸問題。
1.過橋問題
過橋問題一般是多個人或者多個動物需要過河,由於過河時間不同,需要進行合理的安排,使得最終過河時間最短。這個問題有兩個原則:(1)盡量讓時間相近的兩個人一起過橋﹔(2)讓對岸過橋時間最短的人返回。
【例題1】毛毛騎在牛背上過河,他共有甲、乙、丙、丁4頭牛,甲過河要20分鐘,乙過河要30分鐘,丙過河要40分鐘,丁過河要50分鐘。毛毛每次隻能趕2頭牛過河,要把4頭牛都趕到對岸去,最少要多少分鐘?
A.190 B.170 C.180 D.160
解析:甲乙先過河,甲返回,用時30+20=50分鐘。丙丁過河,乙返回,用時50+30=80分鐘。甲乙過河,用時30分鐘。最少要50+80+30=160分鐘。
2.排隊問題
在這類問題中,通常有若干人排隊做某事,要求合理安排順序,使這幾個人排隊等候和完成事情的總時間最少。
【例題2】A、B、C、D四人同時去某單位和總經理洽談業務,A談完要18分鐘,B談完要12分鐘,C談完要25分鐘,D談完要6分鐘。如果使四人留在這個單位的時間總和最少,那麼這個時間是多少分鐘?
A.91分鐘 B.108分鐘 C.111分鐘 D.121分鐘
解析:時間越短越靠前,因此談話順序為DBAC,停留時間為6×4+12×3+18×2+25=121分鐘。
3.任務分配問題
在分配任務時要做到人盡其用,因此讓“相對效率”高的人去做他擅長的事才能確保整體效率是最高的。這類問題有諸多變形,分配原則來自對該問題涉及的核心公式的分析。
【例題3】一個產品生產線分為A、B、C三段,每個人每小時分別完成10、5、6件,現在總人數為71人,要使得完成的件數最多,問:71人的安排分別是( )。
A.14︰28︰29 B.15︰31︰25
C.16︰32︰23 D.17︰33︰21
解析:從命題分析來看,這是一個典型的工作安排問題,首先要明確工作的目標,其次要弄清任務安排的關鍵點。
4.物資集中問題
這類問題通常是:在非閉合的路徑上(線形、樹形等,不包括環形)有多個“點”,每個點之間通過“路”來連通,每個“點”上有一定的“貨物”,要求合理安排把貨物集中到一個“點”上,使得所需的運費最少。或者有一定人數,要求合理設置一個站點,使得各“點”上的人到站點所走的總路程最短。
解決問題時,可通過以下方式判斷方向:路兩側物資總重量小的流向總重量大的(本法則隻適用於非閉合路徑中,與各條路徑的長短無關)。實際操作中,應從中間開始分析,這樣可以更快得到答案。
【例題4】在一條公路上每隔100公裡有一個倉庫,共有5個倉庫,一號倉庫存有10噸貨物,二號倉庫存有20噸貨物,五號倉庫存有40噸貨物,其余兩個倉庫是空的。現在要把所有的貨物集中存放在一個倉庫裡,如果每噸貨物運輸1公裡需要0.5元運輸費,則最少需要運費( )。
A.4500元 B.5000元
C.5500元 D.6000元
解析:如圖所示從中間分析,二號倉庫左側有30噸貨物,三號倉庫右側有40噸貨物,應往三號集中﹔同理比較三、四號倉庫應往四號倉庫集中﹔比較四、五號倉庫應往五號倉庫集中。全部集中到五號倉庫需運費10×400×0.5+20×300×0.5=5000元,選B。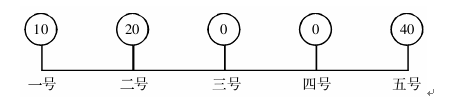
5.貨物裝卸問題
如果有M輛車和N(N>M)個工廠,所需裝卸工的總數就是需要裝卸工人數最多的M個工廠所需的裝卸工人數之和。(若M≧N,則跟車人數為0,把各個點上需要的人相加即為所需要的總人數)
【例題5】一個車隊有三輛汽車,擔負著五家工廠的運輸任務,這五家工廠分別需要7、9、4、10、6名裝卸工,共計36名﹔如果安排一部分裝卸工跟車裝卸,那麼不需要那麼多裝卸工,而隻要在裝卸任務較多的工廠再安排一些裝卸工就能完成裝卸任務,則在這種情況下,總共至少需要多少名裝卸工才能保証各廠的裝卸要求?
A.26 B.27 C.28 D.29
解析:有3輛汽車,最多有3個工廠同時卸貨,即要保証滿足各廠裝卸要求隻考慮需要人數最多的3個工廠同時卸貨需要的人數即可。所以至少需要7+9+10=26名。
三、推理問題
推理問題復雜多變,但都是從給定或隱含條件入手進行推理。把題干給的每一個條件都理解清楚很重要,在每個條件都分析清楚仍不得要領的情況下,要著重分析問題背景隱含的條件。
1.利用題干條件推理
大部分推理問題可根據題干條件直接推理,推理過程需要做簡單計算,合理運用代數工具可簡化推理過程。
【例題1】一個正方體木塊放在桌子上,每一面都有一個數,位於對面兩個數的和都等於13,小張能看到頂面和兩個側面,看到的三個數和為18﹔小李能看到頂面和另外兩個側面,看到的三個數的和為24,那麼貼著桌子的這一面的數是多少?
A.4 B.5 C.6 D.7
解析:小張與小李看到數字之和為:頂面數字的2倍+四個側面數字之和=18+24=42。由於對面兩個數的和都等於13,四個側面數字之和為13×2=26。則頂面數字為(42-26)÷2=8。貼著桌子的底面數字為13-8=5,選B。
2.利用隱含條件推理
在一些較難的推理問題中,線索隱含在題目背景中,找出這個切入點需要對問題背景比較熟悉。
【例題2】小趙、小錢、小孫一起打羽毛球,每局兩人比賽,另一人休息。三人約定每一局的輸方下一局休息。結束時算了一下,小趙休息了2局,小錢共打了8局,小孫共打了5局。則參加第9局比賽的是( )。
A.小趙和小錢 B.小趙和小孫
C.小錢和小孫 D.以上皆有可能
解析:從命題分析來看,三人約定的游戲規則就是本題的推理規則,應該從理解游戲規則開始。
“每一局的輸方下一局休息”,由於每局都會有一個人輸,所以相同的兩個人不會連續比賽兩場﹔任何一人也不會連續休息兩局。還有一點,某人打的總局數等於他和另外兩個人分別打的局數之和,某人休息的局數就應該是另外兩個人打的局數。
因此﹛錢vs孫﹜=2。小錢共打了8局,那麼﹛錢vs趙﹜=8-2=6。小孫共打了5局,﹛孫vs趙﹜=5-2=3。3人總共打了2+6+3=11局。小孫休息了6局,由於休息不能連續,則兩次休息之間至少間隔一場,則隻能是1、3、5、7、9、11這6局,也就是第9局小孫在休息,小錢和小趙在比賽,本題答案為A。
來源:中公教育

 分享到人人
分享到人人 分享到QQ空間
分享到QQ空間










 恭喜你,發表成功!
恭喜你,發表成功!

 !
!





















