2015年公務員考試難題閃開：行程問題

2014年08月06日18:15 手機看新聞

在數學運算中，“行程問題”是歷年考查的重點題型，也是每年都幾乎涉及的常考題型。它要求大家不僅要掌握一些基本知識，還要掌握一定的解題技巧和常考題型的解法?公式。所以“行程問題”就成為很多考生望而生畏的“難點題型”。有關行程問題的方法和題型有很多種，這裡老師主要給大家介紹一種技巧--比例法。它在我們行程問題中有著廣泛地應用，熟練地掌握這種技巧，可以大大提高我們行程問題的准確率。下面結合幾個具體的例題向大家介紹比例法是怎樣應用在我們行程問題之中。

一，基本知識點

1.行程問題基本比例：。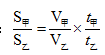

2.t若相同，S與V成正比例﹔V若相同，S與t成正比例﹔S若相等，V與t成反比。

二，典型例題

【例1】（北京2012-82）甲乙兩人早上10點同時出發勻速地向對方工作單位行進，10點30分兩人相遇並繼續以原速度前行。10點54分甲到達乙的工作單位后，立即原速返回自己的工作單位。問甲返回自己的工作單位時，乙已經到了甲的工作單位多長時間？（）

A.42分 B.40分30秒 C.43分30秒 D.45分

【解析】從相遇點到乙的工作單位的這段路程，乙需要30分鐘，甲需要24分鐘，根據比例法，“S相等時，t與V成反比例”可知，甲乙兩人的速度比為30:24=5:4。甲走完一個全程，需要54分鐘，再次利用“S相等時，t與V成反比例”可知，乙走完一個全程需要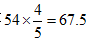（分鐘）。甲返回自己單位時，來回走了兩個全程，所以共需54*2=108 （分鐘），此時乙已經等待了108-67.5=40.5（分鐘），答案為B。

【例2】（國家2011-66）小王步行的速度比跑步慢50%，跑步的速度比汽車慢50%。如果他騎車從A城到B城，再步行返回A城共需要2小時。問小王跑步從A城去B城需要多少分鐘？（）

A.45 B.48 C.56 D.60

【解析】根據題意可知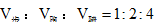。因為騎車，跑步完成的路程都是AB兩地的距離，根據比例法中，“S相等時，V與t成反比”可知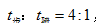，，步行和騎車的時間共有2小時=120分鐘，所以騎車的時間24分鐘。又因為跑步和騎車完成的路程也是AB兩地之間的距離，所以再根據“S相等時，V與t成反比”可知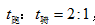，，所以跑步的時間為 24*2=48（分鐘），故答案為B。

【例3】（2010年918聯考-33）小王從家開車上班，汽車行駛10分鐘后發生了故障，小王從后備箱中取出自行車繼續趕路。由於自行車的速度隻有汽車速度的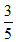，小王比預計時間晚了20分鐘到達單位。如果之前汽車再多行6千米，他就能少遲到10分鐘。問小王從家到單位的距離是多少千米？（）

【解析】將全程分為兩段，第一段距離的速度是汽車的速度，第二段距離的速度是自行車的速度。對於第二段距離，因為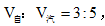，所以根據比例法，“S相等時，V與t成反比”可知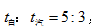，。20分鐘是汽車和自行車的時間差，所以汽車完成第二段距離需要30分鐘，自行車完成第二段距離需要50分鐘。對於6千米的距離，再由“S相等時，V與t成反比”可知，，10分鐘是兩者在6千米上的時間差，所以完成6千米，汽車需要15分鐘，自行車需要25分鐘，進而求得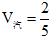（千米/分）。汽車完成全程共需要40分鐘，所以小王從家到單位的距離是（千米），故答案為D。