2015年公務員考試難題閃開：排列組合

在公務員考試中，“排列組合”問題和“行程問題”一樣，是廣大考生最為頭痛的題型，也幾乎是歷年考試的必考重點題型。大家之所以認為排列組合問題難原因有兩點：（1）基礎知識點的遺忘。因為部分考生自從高中畢業之后，就很少再接觸排列組合的知識，所以再應用時就會覺得很陌生，不知從何下手。（2）常考模型的不熟悉。所以建議大家在備考時主要從這兩方面著手。對於基礎知識部分，大家需要掌握兩大原理：加法和乘法原理﹔兩個概念：排列和組合﹔三個公式：排列公式，組合公式和逆向公式。對常考題型，總結主要有捆綁插空模型?錯位重排模型?和插板模型等。下面結合具體例題向大家介紹。

一，捆綁插空模型

（1）基本模型

捆綁法：針對有主體要求在一起或相鄰的問題。解題思路分為兩步

第一步：將要求在一起（或相鄰）的主體捆綁起來看做一個主體，和其余主

體一起排列﹔

第二步：將捆綁起來的主體鬆解，將這些捆綁起來的主體進行排列。

插空法：針對有主體要求在不一起或不相鄰的問題。解題思路分為兩步

第一步：不考慮要求不在一起（或不相鄰）的主體，隻排列無特殊要求的主

體﹔

第二步：將有要求的主體插在已排好順序的主體所形成的空隙中。

（2）典型例題

【例】某人射擊8槍，命中4槍，恰有3槍連續命中的情形有多少種？（ ）

A.720 B.480 C.224 D.20

【解析】題目要求命中的四槍中，恰有3槍連續命中，就是說4槍中，3槍連在一起，

剩余的1槍要和這3槍不在一起。根據我們捆綁插空的模型，在一起的3槍

使用捆綁法，將其捆綁起來看做1個主體﹔另外1槍不得與前面3槍相連，

考慮插空。先將未命中的4槍排列，形成5個空﹔再將命中“3”槍和命中“1”

槍插入其中的2個空中，共有 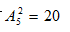（種）情形，故答案是D.

二，錯位重排模型

（1）基本模型

有N封信和N個信封，每封信都不裝在自己的信封裡，可能的方法的種數記為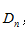。，則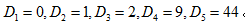

（2）典型例題

【例】（浙江2011-50）四位廚師聚餐時各做了一道拿手菜。現在要求每人去品嘗一道

菜，但不能嘗自己做的那道菜。問共有幾種不同的嘗法？（ ）

A.6種 B.9種 C.12種 D.15種

【解析】此題很多考生會選擇枚舉法解題，但是會花費一定的時間。可以直接應用錯位

重排公式，四個人的錯位重排對應9種。故答案為B。

三，插板模型

（1）基本模型

將M個相同的東西分給N個人，每人至少分一個。則一共有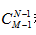 種不同的分法。

（解析：要使每人至少分一個的話，相當於將M個東西分成N堆，這時隻需要在M個相

同的東西之間插N-1個板。）

（2）典型例題

【例1】（國家2010-46）某單位訂閱了30份學習材料發放給3個部門，每一個部

門至少發放9份材料。問一共有多少種不同的發放方法？（ ）

A.12 B.10 C.9 D.7

【解析】先拿出24份材料每個部門發8份，這時變成“6份材料發給3個部門，

每個部門至少發1份”，這是插板的基本模型，所以利用插板法，在5個空中插上2個板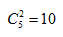：（種）。故答案為B

【例2】將6個相同的蘋果分給3個小朋友，請問一共有多少種分配方法？（ ）

A.16 B.20 C.24 D.28

【解析】先向每一個小朋友“借”一個蘋果，那麼現在總共有6+3=9 （個）蘋

果。此時問題就轉化為“將9個蘋果分配給3個小朋友，為了償還之前借的蘋果，

要求現在分配的時候每個小朋友至少得到1個蘋果”，利用插板法，共有（種）分法。

來源：華圖教育